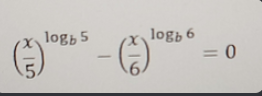
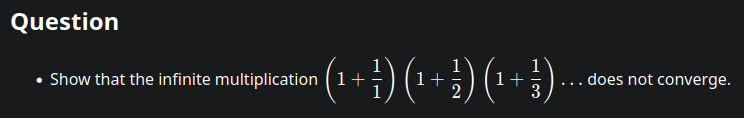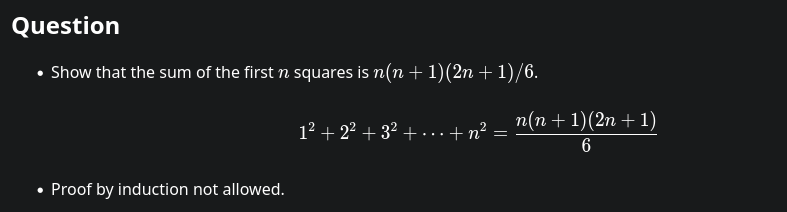Daily Maths Challenges
223 readers
2 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 1 year ago
MODERATORS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
view more: next ›