this post was submitted on 04 Nov 2023
629 points (94.4% liked)
Math Humor
733 readers
1 users here now
Who says math isn't funny? This is a community dedicated to mathematical comedy!
Rules:
- Posts should contain some amount of math(s)
- No NSFW content
- No hate speech, bigotry, etc
Community icon by Icon Arts, licensed under CC BY 3.0
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
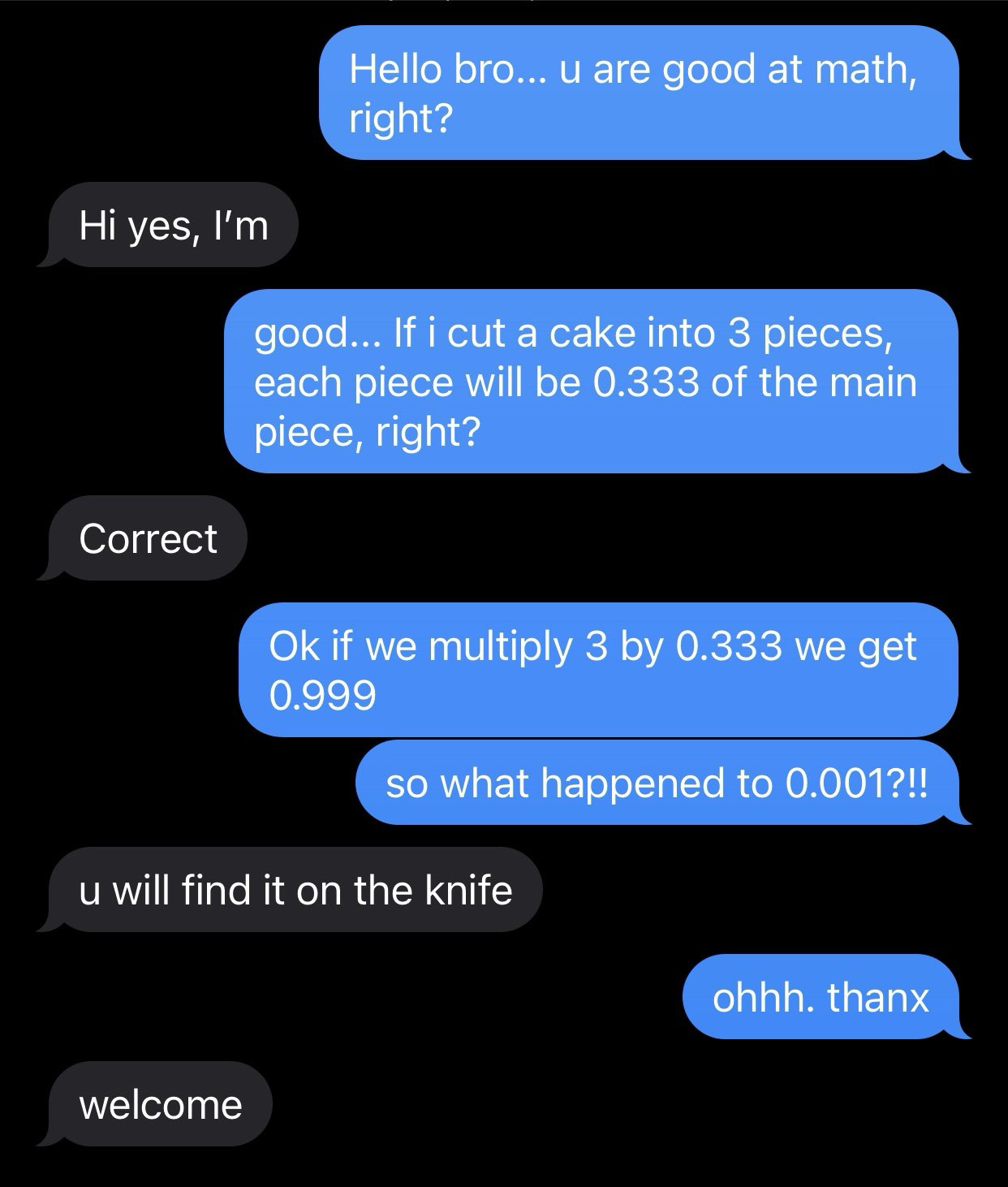
Because it’s not .333, it’s .333… or 1/3 and it’s not .999, it’s .999…, which is the same as 1 🫠. Primes and fractions are weird.
The fun thing is this is just a consequence of how we write numbers. If you used base 12 1/3 would be 0.4. Obviously 0.4 + 0.4 + 0.4 in base 12 is 1.0, so 3 x 0.4 = 1
What's even more fun is that things like 1/5 or 1/10 are recurring decimals in base 12.
You know, this explanation makes it make sense to me a lot more than most of the others I've ever gotten.
I don’t get it. Are you saying the knife is clean?
Yes. The knife is clean if we are cutting exact thirds. As one other user mentioned, base-10 doesn’t allow prime fractions to be conveyed cleanly, so we use repeating decimals to imply that it is a fraction.
Either we live in a world where .333 is correct or we live in a world where knives come out clean when cutting a cake. We can't have both
So that's a no on the infinite cake universe?
Lame.
It's a flaw in how we decribe our numbers
It's not even really a flaw. Just a property. In some sense we've lost the property of uniqueness of decimal representations of numbers that we had with other sets of numbers like integers. In another sense we gain alternate representations for our numbers that may be preferrable (for example 1=1.000... but also 1=0.999...).
Flaw is a bit harsh. Periodic, infinite decimals happen because the denominator is not a multiple of the prime factors of the base and thus will exist in any base.
Not in base infinity.
Infinity is not a number and even if you would use it as a base, you couldn't represent anything other than infinity in a meaningful way.
Infinity^0 is indeterminate and infinity^x with x>0 is exactly infinity.