698
Magic π
(mander.xyz)
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
this post was submitted on 22 Jan 2024
698 points (99.0% liked)
Science Memes
10905 readers
790 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- !abiogenesis@mander.xyz
- !animal-behavior@mander.xyz
- !anthropology@mander.xyz
- !arachnology@mander.xyz
- !balconygardening@slrpnk.net
- !biodiversity@mander.xyz
- !biology@mander.xyz
- !biophysics@mander.xyz
- !botany@mander.xyz
- !ecology@mander.xyz
- !entomology@mander.xyz
- !fermentation@mander.xyz
- !herpetology@mander.xyz
- !houseplants@mander.xyz
- !medicine@mander.xyz
- !microscopy@mander.xyz
- !mycology@mander.xyz
- !nudibranchs@mander.xyz
- !nutrition@mander.xyz
- !palaeoecology@mander.xyz
- !palaeontology@mander.xyz
- !photosynthesis@mander.xyz
- !plantid@mander.xyz
- !plants@mander.xyz
- !reptiles and amphibians@mander.xyz
Physical Sciences
- !astronomy@mander.xyz
- !chemistry@mander.xyz
- !earthscience@mander.xyz
- !geography@mander.xyz
- !geospatial@mander.xyz
- !nuclear@mander.xyz
- !physics@mander.xyz
- !quantum-computing@mander.xyz
- !spectroscopy@mander.xyz
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and sports-science@mander.xyz
- !gardening@mander.xyz
- !self sufficiency@mander.xyz
- !soilscience@slrpnk.net
- !terrariums@mander.xyz
- !timelapse@mander.xyz
Memes
Miscellaneous
founded 2 years ago
MODERATORS
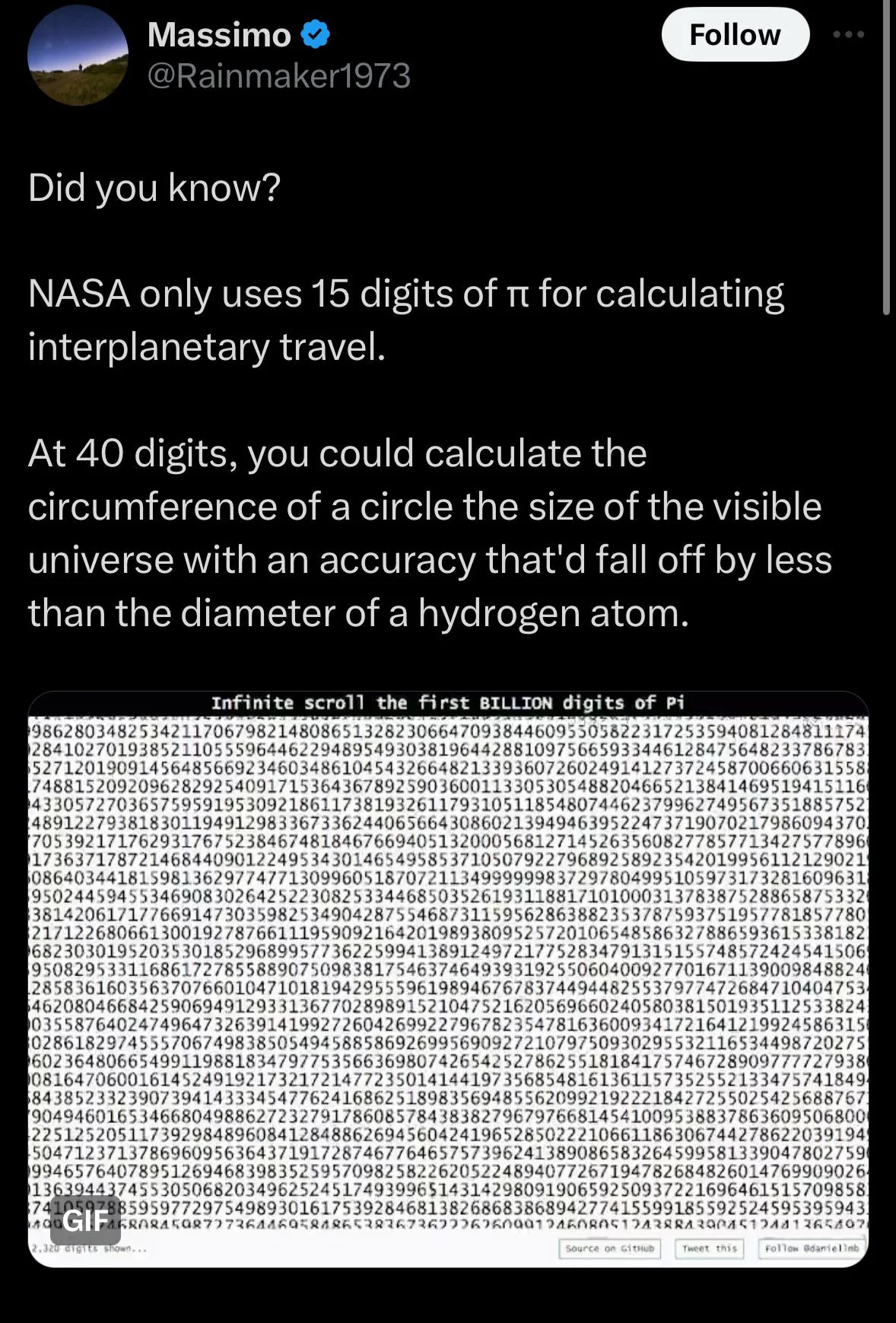
There's a 9 repeating 6 times in there which I'd think is a pretty rare occurrence in pi. I wonder what the longest occurrence of a repeating digit is.
Pi is infinite so every combination/string of numbers is in there, if we calculated enough you could find a billion 2s next to each other
You can look through the first trillion here
https://archive.org/details/pi_dec_1t
Though it’s a bunch of downloading
Not necessarily. It could just become a series of 1's repeating forever. Nothing would require it to contain all strings of numbers.
If that happens in a number, then it is rational. Pi is not rational, so that will never happen in pi.
The point of pi is that it’s non-repeating
Take a look at 0.101001000100001... This number is also non-repeating, but obviously doesn't contain all numbers with finite digits.
The property you're looking for is called to be a normal number. Pi is assumed to be one, but it hasn't yet been proven.
However, in a sense this is an unremarkable property as almost all real numbers are normal. :)
I was just claiming possibility because we haven’t calculated the infinite string
At work at the moment so can't go deep into it. But I think you misunderstand what non repeating numbers mean. Of course there are repeating numbers within pi which is fine, the issue would be if ALL the digits were to simply cycle over and repeat themselves. If however there are a few trillion digits then a series of 1's and 0's for ever, pi is still non repeating
Did you read what I responded to?
I did read it, I also wrote it. Wasn't trying to put you down or anything just sharing a bit of knowledge I found interesting. I know many people (my self included at one point) assumed pi would have to include everything when that just isn't true. Apologies if I did a bad job explaining it though
I wasn’t clear then, it’s not that it has to
It’s that it can until calculated
Looked it up, and it's apparently called the Feynman point after Physicist Richard Feynman (though the story behind that attribution is disputed). https://en.wikipedia.org/wiki/Six_nines_in_pi?wprov=sfla1
That's fascinating. Obviously, there's a series of repeating numbers in there, and one of the numbers would have a highest number of repeats... until further places of pi are determined and another number knocks it off... I assume there's a repeating 1, or 2 that repeats 7 or 8 times,etc... at some point...
On a long enough string I'm guessing... Infinite? Pi isn't a pattern so does it follow the same "if monkeys hade an infinite amount of time to type at a typewriter they'd type Shakespeare"
Well I thought that at first, but it has to be less than infinite since other numbers have to repeat in there as well with at least some occurrence so it's infinite minus something, but since pi goes on infinitely, it's obviously some high number...