To set the scene, I'm talking about this article. My credentials don't really matter, anyone with a cursory understanding of B.Sc.-level computability theory can grok that this is a pile of garbage; however, I do know my way around computational models and I'm in a CS doctorate program, so I know how legitimate research looks like. Or more importantly for the topic I hand, how it DOESN'T look like.

To start off, the first sentence of the article has a CITATION NEEDED next to it.

That's usually a great sign of well-vetted scientific content. The classic LessWrongian style of writing makes it seem like it's some really complicated advanced stuff, but we teach this to CS students fresh out of highschool. It's not rocket science. I will try to explain some of the concepts in layman terms. The most important thing you need to know about Turing machines (TMs) is that they are the standard formalization of what a computer program is - any algorithm can be modeled by a Turing machine.

When a computer scientist says "algorithm" they mean "Turing machine". These are interchangeable. Let me stress this: algorithm is defined as a Turing machine. By definition, it cannot do anything that a TM cannot. We can informally say that an algorithm is a process that can be explained with finite prose, supposed to arrive at some goal in finite time, but that's not a definition.

Now this isn't to say that models stronger than TMs are not theoretically interesting! In fact, computer scientists have been studying many impossible things - we know that it's impossible to tell if an algorithm ever actually stops. Logically impossible. That's the Halting Problem (HALT). You can very easily make a model more powerful than a TM - just give it a magic box that can answer HALT.

In fairness, models that are weaker than full TMs are actually much more interesting and have actual practical applications. Models stronger than TMs cannot have practical applications, as they are physically impossible to achieve...

This is part nonsense and part truism. Yes, mathematical models of algorithms allow doing maths on algorithms, that's the point. The second sentence makes no sense since the author doesn't bother to define what a super-recursive algorithms. But we will get to the "definitions" given...

Also, citation fucking needed - if it allows researchers to study their properties, quote some research.

No citations here, get used to that. To a hopeful reader this might look like a short intro that will be explored in-depth in the later portion of the article. A hopeful reader would be disappointed. This is classical LessWrong style of post - no substance will ever be given.

BTW, the Church-Turing thesis (CTT) cannot be disproven. It says that TMs exactly represent what humans consider as "computable". It's very intuitive, cause TMs are designed to calculate in the same way a human with pen&paper would. But it's not a formal conjecture, cannot be proven or disproven. As we will see later, this crowd treats CTT as some kind of mathematical dogma for some mysterious reason.

Take a look at this word salad:

These three paragraphs are supposed to define what a super-recursive algorithm is. Allegedly. I'd like you to compare it with the definition of an actual TM, also from Wikipedia, which is an actual mathematical definition of a computation model:

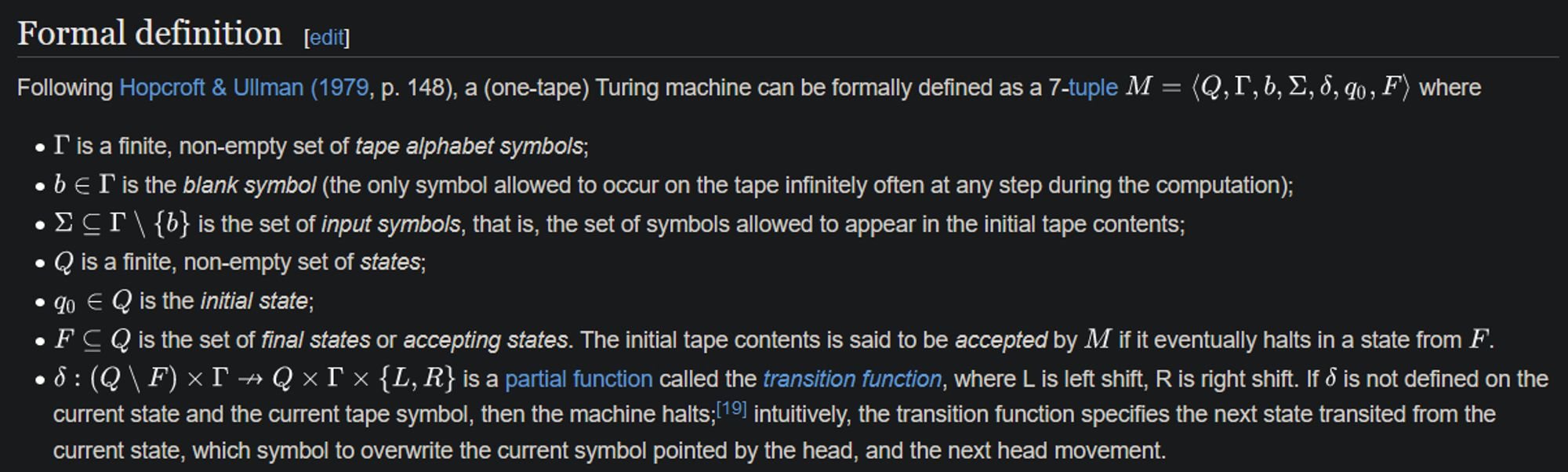
Like it or not, theoretical computer science is basically a branch of mathematics. Mathematical definitions are rarely prose, and for a good reason - prose is inaccurate. It's perfectly fine to talk about math in English, but a useful definition has to be formal. That's literally CS 101. Look at how finite or push-down automata are defined, both well-studied models of computation, and you will see very similar symbols and sets used. This is standard.

You can see this math-avoidance in so many areas of crankery. Famously, quantum physics cranks never give any equations for the bullshit they're peddling, even though theoretical quantum physics requires relatively advanced math and calculus to even define what it talks about. Cranks hate actual math and formalisms precisely because they are precise and rigorous, they leave you no wiggle-room.

Anyone who refuses to provide you with math when speaking about math should be distrusted. Imagine someone telling you they have an amazing new way of building a bridge but refusing to provide any equations that calculate how it can handle load. You shouldn't step on that bridge for fear of your life.

The "definition" given in the informal prose above is useless. An algorithm is DEFINED as "something that a Turing machine computes". If you say that super-recursive algorithms are "algorithms not computable by a Turing machine" then you're saying it's nothing. An empty set. There are no algorithms like that. I can generously read that as "computations of machines stronger than TMs", but then you need to define what such a computation is.

See, the CORE CONTRIBUTION of Turing's seminal paper is that he precisely defined what we mean by "computing" something. For example, we know that we can COMPUTE the value of π up to any decimal place. Turing gave a neat tool of describing:

1. the algorithm, what rules to follow to compute that value;
2. the computation itself, the "paper trail" of a computer executing the algorithm.

This may sound quaint but is actually huge. This enables us to study all sorts of things, for example what it means for some computations to be "harder" or "more expensive" than others - just look at the length of the paper trail! I can prove that my algorithm of computing the n-th digit of π is more efficient than yours, because it uses less theoretical paper for the computation!

The definition of a TM is very elegant - it describes the same things a human can compute if they have access to as much pencil and paper as they want. If you're defining something beyond that, you need to tell me what it is. Without that there's no way of discussing the model - we're just handwaving about some esoteric undefined operation.

The 2nd paragraph is a word salad. Hypercomputation is an umbrella term for "machines stronger than TM", so the definition is cyclical (recursive, hehe (god kill me)). I'd be very happy if you could give me a finite constructive description of a super-recursive algorithm. Spoiler - I will not be happy.

AND ANOTHER THING, I said drunkenly, A SUPERTASK IS A PHILOSOPHICAL CONCEPT. THERE IS NO MATHEMATICAL DEFINITION OF A "SUPERTASK". YOU CAN'T DEFINE A TERM WITH ANOTHER UNDEFINED TERM! You could just as well say that super-recursive algorithms are the ones that frobulate. Same information content.

You might've heard about "supertasks", it's a philosophical term for stuff like the Zeno paradox. There's no such term in mathematics. Also Zeno's paradox has no application to a Turing machine - when talking about TM computations time is quantifiable, there is a notion of a single step taking a single unit of time.

CITATION NEEDED, I screamed into the void.

No idea what "algorithmic schemes" are. The closest actual term in CS I can come up with is an approximation scheme, which is basically a parameterised algorithm, but it doesn't really fit with the rest of the text. An approximation scheme would be "I know how to compute π, but with an error". You give me some value for the error, say 0.1%, and I compute π +- 0.1%. You can give me any value, but for lower errors I will take more time and resources to compute, so e.g. 0.01% accuracy might take twice as long.

"It is necessary to make a clear distinction between bulbulators and those frobulators that are not lightbulbs. No, I will not be taking questions."

"This explains" is some wishful thinking, mate. Inductive TMs are a new, undefined term (which will unfortunately come back), and infinite-time TMs are an actual CS term, but they are ridiculously powerful. I can't draw any relation between them and something the author hasn't defined though.

Infinite-time TMs are, well, TMs that are allowed to spend infinite time to compute something. They can be rigorously mathematically defined, and then you can prove that they know how to, among other things, solve the HALT problem. Of course they exist only in CS theory - we can do math on them and find out what other things would be possible given infinite time, but back in physical reality we don't have infinite time.

OKAY, EXAMPLES. I CAN WORK WITH EXAMPLES.

This is the first time an actually new thing is provided that makes sense. "Limiting recursion" is defined in this paper. It's an interesting model, and showcases the main issue with making any grandiose claims about these.

The idea is that we have a machine that gives us answers that might be incorrect, but after some finite time it will start giving the correct answer and only the correct answer. So if we ask it "what is 2+2" it will say 5, then 17, then 2137, but inevitably after some number of tries it will say 4 and then keep saying 4 forever.

The issue with this is quite obvious - we cannot verify the answer at all. You cannot actually solve a problem with this, because you don't know when to stop asking. It's a calculator that will give you the correct answer to an equation if you press = enough times, but you don't know how many times is enough. It's practically useless - it gives answers you can't verify unless you solve the equation yourself, at which point you didn't need the machine.

I believe this is what the author of the original Wikipedia article believes super-recursive algorithms to be - algorithms that can be wrong indefinitely. Let me reiterate that from a practical standpoint these are utterly worthless. A limiting-recursive machine can be literally wrong FOREVER.

Yes, in the mathematical sense they have to be right eventually, but it can run "empirically forever", i.e. until it exhausts all resources - all energy we have, all available physical space, or literally all of energy everywhere in the absolute physical limit of the heat death of the universe. Entropy is the ultimate clock here, the universe does not have infinite energy to infinitely feed an infinite machine! A computer that gives random results is empirically indistinguishable from this super-recursive one, because time is finite. Time is so, so, finite, and I'm wasting so much of it on this fucking article...

I'm going to skip over most examples - I either can't find their definitions anywhere, or they are basically equivalent to the first one. I need to stop and talk about this gem, though:

This is such an incredible rabbit hole it essentially triggered this entire rant.

Let me start with some science - biological computers are an actual thing. They're extremely cool! The idea is that cells and proteins exhibit some extremely simple and predictable behaviour in nanoscale, so we can "program" logic gates on them. Of course, this is very basic - hardly an actual computer. But it's still a cool thing that we have such a deep understanding of biochemistry we can make these things our toys and try to run the Game of Life on life.

This "evolutionary computer" thing is hardly related to that at all, and is genuinely bonkers. As always, there is no citation linked, but in the References section we can find a single entry by D. Roglic, published in the prestigous peer-reviewed journal of... arxiv. Here's the abomination. Please don't read it, I did and will bear the scars forever.

I don't know if the author is the original author of the super-recursive article, or if they are somehow related, but it's been there since the very first revision! This is basically the underpinning of this article, someone read this revolutionary work and was like "that's it, we need a Wikipedia page for our awesome new concept".

Just look at this abstract:

This must be what actual quantum physicists feel when they see some woo garbage about "quantum energy fields". Where do I even start with this? First of all, just so we're on the same page, anyone can update basically any PDF to arxiv. There is zero review. They probably do remove CAM. A PDF being on arxiv is no higher accolade than having your photo accepted to imgur or your new short story to fanfiction.net.

The first thing that strikes your eyes like a vicious wild animal is the language:

Now, bad English is naturally a low-hanging fruit, so I will only note this once, now at the start. Many people submitting actually useful research are not native speakers and make loads of mistakes. When peer-reviewing papers submitted to conferences you will often find bad quality English, especially if the research team is entirely based in a non-English speaking country. That's fine - there are editors that can help with that, peer-review is also meant to revise some text to make it clearer and more approachable, and the main criterion of review is the merits of the research. There are many steps before a work is actually published in a journal, and at the end these linguistic wrinkles are dealt with.

The author of this PDF uploaded it in 2007. There was plenty of time to show it to someone better versed in English, run it through an editor or at least a spellchecker. This is sloppy and unprofessional.

Let's dive into the "merits" though:

This is straight-up pseudoscience. As I mentioned earlier CTT is a philosophical claim, and no one doing actual computer science spends "great deals of time" gathering evidence for a non-conjecture. We do useful things instead, like filing grant proposals. It's basically "mainstream science was wrong all along!", CS edition.

This Burgin guy is the one to blame for all of this, every road leads to him. Is this entire concept just stemming from a single source? It's a 300-page book that costs $100, I'm not gonna waste my time on it. It would be interesting to see at least excerpts, though.

Burgin appears to be an actual researcher, dealing with logic and AI. His publication record is not great. I can see some "superrecursive" work published at FCS'05 and FCS'06, but it's not clear to me what that conference is? It stands for "International Conference on Foundations of Computer Science". I have never heard of it. Now, there is a very respectable (A*, highest rank) conference called FOCS -- "The Annual IEEE Symposium on Foundations of Computer Science". I don't have enough info to make a definitive claim here, but on first glance it looks really bad. FCS is not even listed in the CORE ranking, which is the standard gauge of conference quality in computer science. (CS is a bit different than most other fields in that people publish mainly on conferences, not in journals - having a paper at an A* conference is a mark of highest-quality research with very high standards of peer-review).

There is probably another dissection/rant lurking in Burgin's work, but I don't have the wine for it now. Back to the arxiv PDF:

TBH arxiv should have the ability to add a CITATION NEEDED to a PDF. Please tell me what challenge these pose to "strong CTT" (btw "weak" and "strong" CTT were never defined and are not standard terms). The claim here is that we cannot simulate DNA MRS on a computer. I'm sure bioinformatics people would be quite shocked by this.

If anyone could provide us with an actual definition of anything Burgin did it would be great, thanks. I'm not even asking for a formal definition anymore. I'm an expert in this field and I cannot even intuit what smITM would be, at least give me a few sentences of prose!

sips wine this is just delightful. "THE DOGMA OF EVOLUTIONARY BIOLOGY". Like reading creationists' claims.

I'm not a biologist, so can't examine if it's true, but I can find plenty of research on SOS response with protein names I can't pronounce, so it looks like a legit field at least.

From a CS standpoint, the fact that you can describe this process in detail (and actual scientists seem to have an even better understanding) is a great sign that it's probably Turing-computable. You're basically describing what steps would need to be simulated to run this on a computer.

I'm going to skip through biology, I can't verify it and it's actually irrelevant to the main claim:

... which fails on its face.

Computers can simulate finite systems. They're quite useful for that, and giant leaps in our understanding of biology, physics, and chemistry are due to the computational power explosion. Transistor be praised. If you want to describe what "simulate" means formally, we can say that we have a TM that from some initial state can simulate what happens in the n-th step for some input n. So we ask "How will this finite system evolve in 17 quants of time"? Computer goes brrr and outputs the solution.

Remember the example of π? This is analogous - mr. computer, what is the n-th digit of π? Computer goes brrr and gives you that digit of π. You can model a biological process if you know how it works and can put the mechanism as a sequence of instructions to a TM, then just tell it to go brrr and simulate n steps. Nothing would point towards a computer NOT being able to take in a state of bacteria and answering what the DNA repair does in N seconds, as long as we have a good enough understanding of the DNA repair process and the enzymes/proteins/biostuff involved.

Remember that TMs are rigorously formally defined. Thanks to the model we know exactly what happens in every step of computation - we can "peer into the box". In particular, we can ask the TM to simulate all steps from 1 to n and get the output for all of them, with an obvious "paper trail" at how we arrived at each step.

The author seems to assume that a lack of "purpose" in bacterial processes is somehow related to the goal of a TM to compute and output a result. This seems like perversed teleological thinking - since this biological process has no "goal" that I can think of it must be somehow ✨special✨.

If you want to get all philosophical, a TM also doesn't have a "goal". It evolves according to a set of instructions, oblivious to what it does, it only knows how to do that. The instructions tell it to go, it goes; they tell it to halt, it halts.

I wouldn't be myself if I didn't include a nit-pick here:

No, we don't "already know". You and your stoned friend don't qualify as "we". If you use "we already know" in a paper it has to either be some fundamental fact everyone learns during their B.Sc., or you better have fucking proved it above.

Now, after all this bullshit, there was a sentence that, get this, MADE SENSE!

Yes! That's coherent! Turing did done proved that! This is exactly what you would need to show! Please tell me how spectacularly you fail to show that!

First sentence is just meaningless in context of CS -- postreplicable and inducive? I'm not sure if it makes any sense in a biology context either.

The second is gibberish. How can you give a result without stopping? You're using a TM model with an output tape. The TM will also write something there before halting, and then signal "I'm done" with the halt. Definition of an output of an algorithm is "what is present on the output tape after the TM halts". Without a halt signal there can be no result, definitionally.

This is why A FORMAL DEFINITION of what you mean by "give a result" is crucial. Does your DNA-based system have a different definition of result? I am not skipping over any crucial points here, mind you, the author never defined what sEC~sos~ even is, much less how it computes a result.

Well, this is gold. First of all, my brother in Turing, you cannot say "according to definition" if you DIDN'T PROVIDE A DEFINITION!!! I cannot stress this enough, nowhere before is "result of sEC~sos~" defined!

Second, you're so close - elaborate what happens when the TM doesn't stop?

The halting problem is a fundamental unsolvable problem. It's literally impossible to tell for an arbitrary computer program whether it will stop or loop forever. The above claim is a good demonstration of why a naive approach of "just run it" is NOT an answer! Sure, if the TM is nice and actually stops you will know that it stops. But if it doesn't... when can you be certain? At what point can you say "it definitely loops" and not lie? You waited for 3 hours, but it just might be that it terminates after 4h. Or in general, "the time you have" + 1.

What mr. Roglic did is he described a process that goes "it didn't stop yet!" while the TM spins, but apparently because it keeps "giving a result of 0", whatever that means, while the inner TM is going, it's somehow special.

But... we can write a normal program that does this. A TM can just output a 0 on the tape every other step. No biggie.

Let me refolmulate it: imagine I start loading a webpage which we're not sure if it's broken or not, but every second while it's loading I shout "NOT YET!". According to this PDF I solved the halting problem.

There are numerous other problems with this "proof". You would need to show how to actually implement a TM inside of the DNA repair system to even claim it can do the same stuff as a TM does -- currently the paper doesn't even show that this system is at least as strong as a TM, much less stronger! How can we give input to this system? What do we consider the output? How do you measure how much memory it uses? There's so many undefined aspects of this system it's basically as good as just making shit up as we go.

The rest of the PDF hinges of the above "proof", so it can be dismissed at this point. Not only does it not prove the central claim, it doesn't even define what a super-recursive algorithm is and how it'd be different from just the Π~1~^1^ level of arithmetical hierarchy. Oh, I didn't mention that - CS people actually have a formal model of what it means to be "stronger than a TM" with Turing degrees and the arithmetical hierarchy. I have no reason to believe mr. Roglic has any familiarity with those.

There is one more gem I wanted to show:

First of all, a TM doesn't tackle the notion of "mistakes" because why would it. We just say a program does a computation and then analyse that computation. If it actually computes a different function than desired, that's an external issue, not the issue of the model itself.

Like, if I build a plane, and the plane crashes and burns, that's an issue of my planebuilding, not that gravity and air dynamics "embody the idea of perfection" and leave "no place for engineering mistakes".

Second, "evolutionary program of the Nature leaves this theory in its orthodoxy" is now my go-to response if I ever dislike an idea. Slap this on your next peer-review. How can you even argue with such poignant statements.

I also find it delightful that in the seminal paper A. Turing defined the end of a computation as the machine constantly looping between two cells. So quite literally it "produces a result without ever stopping", the key distinction of a super-recursive machine it seems.

Concluding this thorough review due to shortage of wine, I will make the controversial yet brave observation that if this is one of the core works underpining the Super-recursive article, then, to use a technical term, it's a load of shite.

Let us leave this "theory" in its orthodoxy.